Tidak Ada Titik Sudut
Sifat ketiga dari bangun ruang tabung adalah tidak ada titik sudut. Seperti yang kita tahu bahwa bangun ruang dapat terbentuk atau terbangun dari dua buah lingkaran yang terletak pada bagian alas dan tutup tabung yang dipisahkan oleh selimut tabung. Oleh sebab itu, sama halnya dengan lingkaran yang tidak memiliki titik sudut, sehingga bangun ruang juga tidak memiliki titik sudut.
Tidak adanya titik sudut pada tabung bisa dibilang berbeda dengan bangun ruang lainnya yang di mana memiliki titik sudut yang cukup banyak, seperti kubus, balok, dan lain-lain. Meskipun tidak memiliki titik sudut, tetapi bangun ruang tabung masih dapat terlihat dalam bentuk 3 dimensi karena memiliki pemisah lingkaran alas dan tutup.
Bangun ruang tabung merupakan sebuah bangun ruang yang dapat terbentuk dari gabungan antara bangun datar persegi panjang dan bangun datar lingkaran. Maka dari itu, jaring-jaring dari tabung terdiri dari persegi panjang dan dua buah lingkaran (alas dan tutup). Tabung yang terbentuk dari dua buah lingkaran, maka ketika menghitung volume dan keliling tabung tidak lepas dari rumus lingkaran.
Bangun ruang tabung ini pada dasarnya sering kali kita jumpai di rumah, warung, rumah sakit, dan lain-lain. Oleh sebab itu, bisa dikatakan bahwa bangun ruang tabung sudah tak asing lagi bagi setiap manusia.
Sumber: Dari berbagai macam sumber
Kelebihan Mesin Cuci 1 dan 2 Tabung
Membedakan dua produk akan jadi sulit bila Anda tidak tahu secara detail informasi barang tersebut. Sama halnya dengan mesin cuci 1 tabung dan 2 tabung memiliki perbedaan terlepas dari penggunaan tabungnya. Berikut perbedaan mesin cuci 1 dan 2 tabung :
Adanya Lingkaran pada Bagian Alas dan Tutup Tabung
Ciri ketiga dari bangun ruang tabung adalah adanya alas dan tutup pada tabung yang berbentuk lingkarang. Pada bagian sisi alas dan sisi tutup tabung berupa lingkaran. Uniknya lagi, lingkaran yang dijadikan alas dan tutup tabung pasti memiliki ukuran yang sama satu sama lain. Oleh karena itu, ketika menghitung keliling lingkaran, kita hanya menghitung salah satu lingkaran saja dan tak perlu menghitung kedua lingkaran alas dan tutup tabung.
Tidak hanya itu saja, bagian alas dan tutup tabung ini menjadi tanda bahwa dalam bangun ruang tabung ini dibentuk dengan dua lingkaran. Tanpa adanya kedua lingkaran itu, suatu bangun ruang tabung tidak akan terbentuk. Meskipun lingkaran berperan penting dalam terbentuknya bangun ruang tabung, tetapi tanpa adanya persegi panjang (sebagai selimut tabung) tabung tidak akan terbentuk.
Pada dasarnya, setiap bangun ruang pasti memiliki jaring-jaring. Begitu pun dengan bangun ruang tabung juga memiliki jaring-jaring yang terdiri dari dua buah lingkaran dan satu buah persegi panjang. Berikut ini contoh jaring-jaring bangun ruang tabung.
Bangun ruang tabung memiliki dua jenis, yaitu tabung terbuka dan tabung tertutup.
Tabung terbuka adalah jenis tabung yang di mana salah satu sisi tutupnya atau sisi alasnya terbuka atau sisi alas dan sisi tutupnya dua-duanya terbuka.
Tabung tertutup adalah jenis tabung yang di mana seluruh bagian dan sisinya semuanya tertutup.
Volume pada bangun ruang tabung dapat dihitung dengan rumus sebagai berikut
V = Luas alas x tinggi
Melakukan Pengujian
Tabung reaksi berfungsi juga untuk pengujian kualitatif. Inilah mengapa tabung reaksi harus selalu ada di dalam setiap laboratorium sehingga pengujian kualitatif dapat berjalan dengan sempurna.
Baca juga: Pengertian Laboratorium Beserta Fungsi dan Jenisnya
Keliling Alas Atau Tutup Tabung
Untuk menghitung alas atau tutup tabung dapat dihitung menggunakan rumus sebagai berikut:
Bangun ruang tabung atau silinder memiliki beberapa unsur yang terdiri dari, sisi tabung, selimut tabung, jari-jari tabung, diameter tabung, dan tinggi tabung.
Tidak Ada Titik Sudut
Sifat ketiga dari bangun ruang tabung adalah tidak ada titik sudut. Seperti yang kita tahu bahwa bangun ruang dapat terbentuk atau terbangun dari dua buah lingkaran yang terletak pada bagian alas dan tutup tabung yang dipisahkan oleh selimut tabung. Oleh sebab itu, sama halnya dengan lingkaran yang tidak memiliki titik sudut, sehingga bangun ruang juga tidak memiliki titik sudut.
Tidak adanya titik sudut pada tabung bisa dibilang berbeda dengan bangun ruang lainnya yang di mana memiliki titik sudut yang cukup banyak, seperti kubus, balok, dan lain-lain. Meskipun tidak memiliki titik sudut, tetapi bangun ruang tabung masih dapat terlihat dalam bentuk 3 dimensi karena memiliki pemisah lingkaran alas dan tutup.
Bangun ruang tabung merupakan sebuah bangun ruang yang dapat terbentuk dari gabungan antara bangun datar persegi panjang dan bangun datar lingkaran. Maka dari itu, jaring-jaring dari tabung terdiri dari persegi panjang dan dua buah lingkaran (alas dan tutup). Tabung yang terbentuk dari dua buah lingkaran, maka ketika menghitung volume dan keliling tabung tidak lepas dari rumus lingkaran.
Bangun ruang tabung ini pada dasarnya sering kali kita jumpai di rumah, warung, rumah sakit, dan lain-lain. Oleh sebab itu, bisa dikatakan bahwa bangun ruang tabung sudah tak asing lagi bagi setiap manusia.
Sumber: Dari berbagai macam sumber
Hasil Pencarian Tabung Induksi Tabung
Maaf, barangnya tidak ketemu
Coba cek lagi kata pencarianmu.
Tabung Vacutainer berfungsi untuk menampung darah ketika terlekat pada jarum suntik. Terdapat berbagai jenis tabung berdasarkan warna tutup dan zat aditifnya, yang digunakan untuk menjaga kelangsungan hidup sampel darah atau memisahkan komponennya untuk tujuan pemeriksaan kimia, hematologi, mikrobiologi, dan lainnya.
Untuk kegunaan lain, lihat
Tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Tabung memiliki 3 sisi dan 2 rusuk.
Kedua lingkaran disebut sebagai alas dan tutup tabung serta persegi panjang yang menyelimutinya disebut sebagai selimut tabung.
Definisi dan hasil dalam bagian tersebut diambil dari teks pada tahun 1913, Bidang dan Geometri Padat ditemukan oleh George Wentworth dan David Eugene Smith (Wentworth & Smith 1913).
Permukaan tabung adalah permukaan yang terdiri dari semua titik pada baris yang sejajar dengan garis yang diketahui dan melewati tetap kurva pesawat dalam pesawat tidak sejajar dengan garis yang diberikan. Pada garis tersebut kelompok garis sejajar atau disebut juga elemen permukaan tabung. Dari sudut pandang kinematika jika diberi kurva bidang yang disebut directrix. Permukaan Tabung adalah permukaan yang dilacak oleh sebuah garis yang disebut generatrix bukannya dalam bidang directrix, yang sejajar dengan dirinya sendiri dan selalu melewati directrix. Posisi tertentu dari matrik generatrik adalah elemen permukaan tabung.
Bagian Tabung adalah terpotong nya permukaan tabung dengan bagian bidang. Kurva merupakan jenis dari penampang bidang. Bagian Tabung pada bidang yang berisi dua elemen tabung disebut jajaran genjang.[1] Bagian tabung dari tabung biasa adalah selimut alas yang berbentuk persegi panjang.[1]
Bagian Tabung di mana bidang yang terpotong dan tegak lurus terhadap semua elemen tabung.[2] Bagian kanan tabung adalah lingkaran maka tabung tersebut adalah tabung yang melingkar. Secara umum, jika bagian kanan tabung adalah bagian yang berbentuk kerucut (parabola, elips, hiperbola) maka tabung padat masing-masing disebut sebagai parabola, elips, dan hiperbolik.
Tabung berbentuk melingkar kanan dengan penampang tabung yang berbentuk elips, eksentrisitas e dari penampang tabung dan sumbu semi-mayor a dari penampang tabung bergantung pada jari-jari tabung r dan sudut α antara bidang garis potong dan sumbu tabung dengan cara sebagai berikut:
Secara dirumuskan dengan prinsip yang sama volume setiap tabung adalah hasil perkalian dari luas alas dan tinggi. Misalnya tabung berbentuk elips dengan alas bersumbu semi mayor a pada sumbu semi minor b dan tinggi t dengan rumus volume V = πr²×t. Hasil untuk tabung elips dapat diperoleh dengan bentuk integral dimana sumbu tabung diambil sebagai sumbu x dan L(x) = L luas setiap penampang elips dengan dirumuskan sebagai berikut:
Dengan menggunakan koordinat tabung, volume tabung berbentuk lingkaran dapat dihitung dalam bentuk integral yaitu
Bagian ini memerlukan
. Anda dapat membantu dengan
(Inggris) Weisstein, Eric W. "Tabung". MathWorld.
Untuk lebih memahami keunikan tabung, mari kita bandingkan dengan beberapa bangun ruang lainnya:
- Tabung memiliki alas dan tutup yang sejajar dan sama besar, sedangkan kerucut hanya memiliki satu alas dan satu titik puncak.
- Selimut tabung berbentuk persegi panjang jika dibuka, sementara selimut kerucut berbentuk juring lingkaran.
- Volume tabung lebih besar daripada kerucut dengan alas dan tinggi yang sama.
- Tabung memiliki sisi lengkung (selimut), sedangkan semua sisi balok datar.
- Tabung tidak memiliki titik sudut, sementara balok memiliki 8 titik sudut.
- Alas dan tutup tabung berbentuk lingkaran, sedangkan alas dan tutup balok berbentuk persegi panjang.
- Alas dan tutup tabung selalu berbentuk lingkaran, sedangkan prisma bisa memiliki alas berbentuk segitiga, segiempat, atau segi banyak lainnya.
- Tabung tidak memiliki titik sudut, sementara prisma memiliki titik sudut sesuai bentuk alasnya.
- Selimut tabung berbentuk lengkung, sedangkan sisi tegak prisma berbentuk persegi panjang.
- Tabung memiliki alas dan tutup yang datar, sedangkan bola seluruh permukaannya melengkung.
- Tabung memiliki tinggi yang dapat diukur, sementara bola tidak memiliki tinggi.
- Volume tabung dihitung dengan πr²t, sedangkan volume bola dihitung dengan 4/3πr³.
Tidak sedikit orang yang masih belum tahu cara menggunakan mesin cuci dengan benar. Mesin cuci sendiri merupakan perangkat elektronik yang paling banyak orang gunakan. Agar memiliki pakaian yang selalu bersih, kehadiran alat ini menjadi sangat penting dalam setiap rumah.
Menjadi Wadah Bahan Kimia
Di dalam laboratorium pasti terdapat banyak bahan kimia. Untuk mencampur, menampung, dan memanaskan bahan kimia dalam kecil, Anda dapat menggunakan tabung reaksi. Namun perlu diingat bahwa penggunaan tabung reaksi menjadi wadah bahan kimia hanya dalam jumlah yang kecil saja.
Memiliki 2 Buah Rusuk
Ciri kedua dari bangun ruang tabung adalah memiliki 2 buah rusuk yang letaknya berada di bagian alas dan tutup tabung dan berupa lengkungan garis lingkaran. Dengan adanya dua buah rusuk ini, kita jadi tahu bahwa garis lengkungan ini akan memengaruhi ukuran jari-jari bangun ruang tabung. Selain itu, tanpa adanya dua buah rusuk, kita tidak akan tahu letak lingkaran berada di mana karena tidak ada garis lengkungan.
Ciri tabung yang satu ini bisa dibilang sebagai pemberitahu letak dari lingkaran itu berada. Dua buah rusuk menjadi penting karena lingkaran merupakan salah satu bangun datar yang dapat membentuk bangun ruang tabung dan lingkaran sudah menjadi bagian dari jaring-jaring tabung.
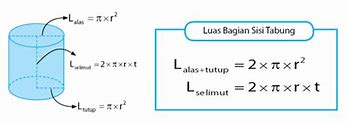
Luas Permukaan Tabung
Untuk menghitung luas permukaan tabung dapat dihitung dengan cara menjumlahkan luas ketiga sisinya.
Luas permukaan tabung = Luas alas + Luas tutup + Luas selimut tabung
Luas selimut tabung = 2 x 𝜋 x r x t























